Soru Sor
Sorunu sor hemen cevaplansın.
# Üçgenin Özellikleri; # Üçgen Nedir ? (Detay) # (ABC Üçgeni)=[AB]U[AC]U[CB] DIŞ BÖLGE # Bir Üçgenin Temel Elemanları # Bir Üçgenin Yardımcı Elemanları # Üçgenin Kenarları Arasındaki Bağlantılar # Üçgenin Açıları Arasındaki Bağlantılar # Üçgenin Kenar Uzunluklar ve Açıları Arasındaki Bağlantılar # Üçgenin Çeşitleri # 1.Kenarlarına Göre Üçgenler # 2.Açılarına Göre Üçgenler # Üçgenin Alanını ve Çevresini Bulma # Ç = a + b + c # ÇÖZÜMLÜ SORULAR
Üçgen Nedir ? (Özet) : Düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşiminden oluşan geometrik şekle üçgen denir.
1. Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir.
2. Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir.
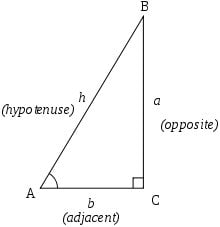
3. Bir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamına eşittir. Buna Pisagor Teoremi denir.
Bir doğru üzerinde olmayan (doğrusal olmayan) A,B,C gibi üç noktanın birleşiminden oluşan kapalı şekle ÜÇGEN denir.
Bir üçgen noktalar kümesidir ve içinde bulunduğu düzlemi üç ayrı noktalar kümesine ayırır.
Bunlar;
a)Üçgenin İçinde Kalan Noktalar Kümesi
b)Üçgenin Kendisi
c)Üçgenin Dışında Kalan Noktalar Kümesi
1.Üçgenin Kenarları: [BC],[AC},[AB] doğru parçalarına “Üçgenin Kenarları” denir. Kenar uzunlukları karşılarındaki açıların kenarlarıyla adlandırılırlar.
2.Üçgenin İç Açıları: Üçgenin iki kenarının oluşturduğu her bir açı “Üçgenin İç Açısı” olarak adlandırılır. Bir üçgenin iç açıları toplamı 180º`dir.
3.Üçgenin Dış Açıları: Üçgenin iç açılarının komşu bütünleri olan açılara “Üçgenin Dış Açıları” denir. Bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir. Bir üçgenin iç açısıyla dış açısının toplamı 180º`dir. Bir üçgenin dış açıları toplamı ise 360º`dir.
1.Üçgenin Yüksekliği: Üçgenin bir köşesinden karşı tarafa indirilen, köşe ile kenar arasında aklan doğru parçasına “Üçgenin Yüksekliği” denir.”H” ile gösterilir.
2.Üçgenin Kenar Ortayları: Üçgenin bir köşe ile bu köşenin karşısındaki kenarın orta noktasını birleştiren doğru parçasına “Üçgenin Kenar Ortayı” denir. “V” ile gösterilir.
3.Üçgenin Açı Ortayı: Üçgenin açılarını iki eş açıya bölen doğruların,köşe ile kenar arasında kalan doğru parçasına “ÜÇGENİN AÇI ORTAYI” denir. ” N” ile gösterilir.
Bir üçgende iki kenarın uzunlukları toplamı üçüncü kenar uzunluğundan büyük; iki kenar uzunluğunun farkı, üçüncü kenarı uzunluğunda küçüktür.
Bir üçgende, bir köşedeki iç açı ile diş açının toplamı 180º`dir.
Bir üçgende, bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
Bir üçgende ölçüsü büyük olan kenar karşısında büyük açı, küçük olan kenar karşısında küçük kenar vardır.
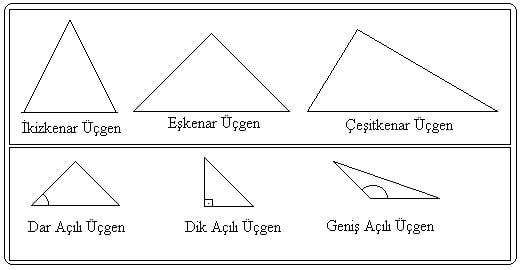
a)Çeşit Kenar Üçgen: Üçgenin kenarlarının hepsi farklıysa bu üçgene “Çeşit Kenar Üçgen” denir.
b)İkiz Kenar Üçgen: Üçgenin kenarlarının iki tanesi eşit olan üçgene“İkiz Kenar Üçgen” denir. Bir ikizkenar üçgenin, taban açıların ölçüleri birbirine eşittir.
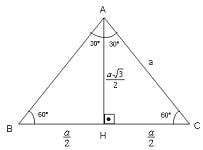
c)Eşkenar Üçgen: Üçgenin kenarlarının hepsi eşit olan üçgene “Eşkenar Üçgen” denir. Bir eşkenar üçgenin iç açıları 60 `dir.
a)Dar Açılı Üçgen:Üçgenin açılarından her birinin ölçüsü 90º`den küçük olan üçgene “Dar Açılı Üçgen” denir.
b)Geniş Açılı Üçgen: Bir açısı geniş açı olan üçgene “Geniş Açılı Üçgen” denir.
c)Dik Açılı Üçgen: Açılarından birisi dik açı olan üçgene “Dik Açılı Üçgen” denir.
Üçgenin çevresini bulabilmek için kenarlar toplanır.
Üçgenin alanını bulmak için yükseklikle kenar çarpılır ve ikiye bölünür.
h x a h x b h x c
1)Tepe açısı 58º olan bir ikiz kenar üçgenin taban açılarından birinin ölçüsünü yazın.
Bir üçgenin iç açıların toplamı 180º ise ve üçgenimiz ikiz kenar üçgen ise
Taban açısı+Taban açısı+Tepe açısı=180º
2 Taban açısı+58º=180º
2 Taban açısı=180º-58º
2 Taban açısı=122º
Taban açısı=61º olur.
2) Yandaki üçgenin, taban açılarından biri 78º,tepe açısı ise 22ºise öbür açıyı bulunuz.
22˚ Üçgenin iç açıları toplamı=180º
22º+78º+xº=180º
100º+xº =180º
x =80º
78˚ x˚
3)İki komşu bütünler açının ölçüleri ardışık tek sayı ise bu açıların farkı kaç derecedir?
2x+1 , 2x+3 ÞArdışık Tek Sayılar 180˚ ÞBütünler Açı
2x+1+2x+3=180˚
4x+4=180˚ 2x+1= 44x2+1Þ89˚
4x=180˚-4˚ Þ
4x=176˚ 2x+3= 44x2+3Þ91˚
x=44˚
4)Yandaki şekilde harflerle belirtilen açıları, hangi açının özelliğiyle 130˚ 50˚
bulduğunuzu belirterek yazınız. A B
A=50ºÞÇünkü 50˚ açısıyla ters açı konumundadırlar. C
B=130ºÞÇünkü 130˚ açısıyla ters açı konumundadırlar. D E
C=50˚ÞÇünkü A açısıyla iç ters açı konumundalar.
D=50˚ÞÇünkü A açısıyla yöndeş açı konumundalar.
E=130˚ÞÇünkü 130˚ açısıyla dış ters açı konumundalar.
5)Bir üçgen tarlanın ölçüleri 10x20x30 km`dir. Çiftçi tarlanın çevresini üç kat telle sarmak isterse ne kadar tel almalıdır?
Alınacak Tel=Üçgenin Çevresix3
Alınacak Tel=(30+20+10)x3
Alınacak Tel=60x3
Alınacak Tel=180 km tel alınması gerekir.
6)Bir üçgenin kenarı 5 cm, yüksekliği ise 4 cm ise bu üçgenin alanı kaç cm ’dir?
Üçgenin alanı=(5x4)/2
Üçgenin Alanı=20/2
Üçgenin Alanı=10cm²‘dir.
7)Bir eşkenar, çeşitkenar, ikizkenar üçgenin çevrelerini nasıl bulurdunuz?(Formülleri)
Eşkenar Üçgen=3a
Çeşitkenar Üçgen=a+b+c
İkizkenar Üçgen=2a+b
8)Bir üçgenin özelliklerinden olan kenarları arasındaki bağlantıları genelleyin.
b+c>a , a+c>b , a+b>c Þİki kenarın uzunlukları toplamı üçüncü kenar uzunluğundan büyüktür.
b-c
Tarih: 2016-03-02 01:56:59 Kategori: Geometri
Soru Tarat
Kitaptan sorunu tarat hemen cevaplansın.
Sorunu sor hemen cevaplansın.
Üçgen Nedir
Bu Yazıda Neler Var:
Üçgenin Özellikleri;
1. Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir.
2. Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir.
3. Bir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamına eşittir. Buna Pisagor Teoremi denir.
Üçgen Nedir ? (Detay)
Bir doğru üzerinde olmayan (doğrusal olmayan) A,B,C gibi üç noktanın birleşiminden oluşan kapalı şekle ÜÇGEN denir.
(ABC Üçgeni)=[AB]U[AC]U[CB] DIŞ BÖLGE
Bir üçgen noktalar kümesidir ve içinde bulunduğu düzlemi üç ayrı noktalar kümesine ayırır.
Bunlar;
a)Üçgenin İçinde Kalan Noktalar Kümesi
b)Üçgenin Kendisi
c)Üçgenin Dışında Kalan Noktalar Kümesi
Bir Üçgenin Temel Elemanları
1.Üçgenin Kenarları: [BC],[AC},[AB] doğru parçalarına “Üçgenin Kenarları” denir. Kenar uzunlukları karşılarındaki açıların kenarlarıyla adlandırılırlar.
2.Üçgenin İç Açıları: Üçgenin iki kenarının oluşturduğu her bir açı “Üçgenin İç Açısı” olarak adlandırılır. Bir üçgenin iç açıları toplamı 180º`dir.
3.Üçgenin Dış Açıları: Üçgenin iç açılarının komşu bütünleri olan açılara “Üçgenin Dış Açıları” denir. Bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir. Bir üçgenin iç açısıyla dış açısının toplamı 180º`dir. Bir üçgenin dış açıları toplamı ise 360º`dir.
Bir Üçgenin Yardımcı Elemanları
1.Üçgenin Yüksekliği: Üçgenin bir köşesinden karşı tarafa indirilen, köşe ile kenar arasında aklan doğru parçasına “Üçgenin Yüksekliği” denir.”H” ile gösterilir.
2.Üçgenin Kenar Ortayları: Üçgenin bir köşe ile bu köşenin karşısındaki kenarın orta noktasını birleştiren doğru parçasına “Üçgenin Kenar Ortayı” denir. “V” ile gösterilir.
3.Üçgenin Açı Ortayı: Üçgenin açılarını iki eş açıya bölen doğruların,köşe ile kenar arasında kalan doğru parçasına “ÜÇGENİN AÇI ORTAYI” denir. ” N” ile gösterilir.
Üçgenin Kenarları Arasındaki Bağlantılar
Bir üçgende iki kenarın uzunlukları toplamı üçüncü kenar uzunluğundan büyük; iki kenar uzunluğunun farkı, üçüncü kenarı uzunluğunda küçüktür.
Üçgenin Açıları Arasındaki Bağlantılar
Bir üçgende, bir köşedeki iç açı ile diş açının toplamı 180º`dir.
Bir üçgende, bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
Üçgenin Kenar Uzunluklar ve Açıları Arasındaki Bağlantılar
Bir üçgende ölçüsü büyük olan kenar karşısında büyük açı, küçük olan kenar karşısında küçük kenar vardır.
Üçgenin Çeşitleri
1.Kenarlarına Göre Üçgenler
a)Çeşit Kenar Üçgen: Üçgenin kenarlarının hepsi farklıysa bu üçgene “Çeşit Kenar Üçgen” denir.
b)İkiz Kenar Üçgen: Üçgenin kenarlarının iki tanesi eşit olan üçgene“İkiz Kenar Üçgen” denir. Bir ikizkenar üçgenin, taban açıların ölçüleri birbirine eşittir.
c)Eşkenar Üçgen: Üçgenin kenarlarının hepsi eşit olan üçgene “Eşkenar Üçgen” denir. Bir eşkenar üçgenin iç açıları 60 `dir.
2.Açılarına Göre Üçgenler
a)Dar Açılı Üçgen:Üçgenin açılarından her birinin ölçüsü 90º`den küçük olan üçgene “Dar Açılı Üçgen” denir.
b)Geniş Açılı Üçgen: Bir açısı geniş açı olan üçgene “Geniş Açılı Üçgen” denir.
c)Dik Açılı Üçgen: Açılarından birisi dik açı olan üçgene “Dik Açılı Üçgen” denir.
Üçgenin Alanını ve Çevresini Bulma
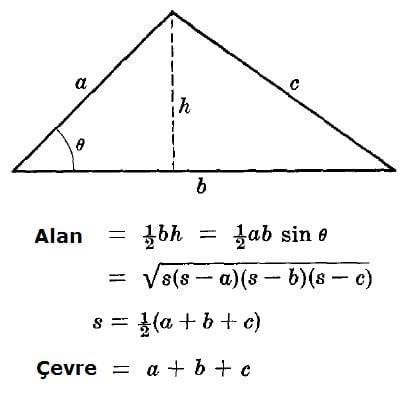
Üçgenin çevresini bulabilmek için kenarlar toplanır.
Ç = a + b + c
Üçgenin alanını bulmak için yükseklikle kenar çarpılır ve ikiye bölünür.
h x a h x b h x c
A= ------- = ------- = -------
2 2 2
ÇÖZÜMLÜ SORULAR
1)Tepe açısı 58º olan bir ikiz kenar üçgenin taban açılarından birinin ölçüsünü yazın.
Bir üçgenin iç açıların toplamı 180º ise ve üçgenimiz ikiz kenar üçgen ise
Taban açısı+Taban açısı+Tepe açısı=180º
2 Taban açısı+58º=180º
2 Taban açısı=180º-58º
2 Taban açısı=122º
Taban açısı=61º olur.
2) Yandaki üçgenin, taban açılarından biri 78º,tepe açısı ise 22ºise öbür açıyı bulunuz.
22˚ Üçgenin iç açıları toplamı=180º
22º+78º+xº=180º
100º+xº =180º
x =80º
78˚ x˚
3)İki komşu bütünler açının ölçüleri ardışık tek sayı ise bu açıların farkı kaç derecedir?
2x+1 , 2x+3 ÞArdışık Tek Sayılar 180˚ ÞBütünler Açı
2x+1+2x+3=180˚
4x+4=180˚ 2x+1= 44x2+1Þ89˚
4x=180˚-4˚ Þ
4x=176˚ 2x+3= 44x2+3Þ91˚
x=44˚
4)Yandaki şekilde harflerle belirtilen açıları, hangi açının özelliğiyle 130˚ 50˚
bulduğunuzu belirterek yazınız. A B
A=50ºÞÇünkü 50˚ açısıyla ters açı konumundadırlar. C
B=130ºÞÇünkü 130˚ açısıyla ters açı konumundadırlar. D E
C=50˚ÞÇünkü A açısıyla iç ters açı konumundalar.
D=50˚ÞÇünkü A açısıyla yöndeş açı konumundalar.
E=130˚ÞÇünkü 130˚ açısıyla dış ters açı konumundalar.
5)Bir üçgen tarlanın ölçüleri 10x20x30 km`dir. Çiftçi tarlanın çevresini üç kat telle sarmak isterse ne kadar tel almalıdır?
Alınacak Tel=Üçgenin Çevresix3
Alınacak Tel=(30+20+10)x3
Alınacak Tel=60x3
Alınacak Tel=180 km tel alınması gerekir.
6)Bir üçgenin kenarı 5 cm, yüksekliği ise 4 cm ise bu üçgenin alanı kaç cm ’dir?
Üçgenin alanı=(5x4)/2
Üçgenin Alanı=20/2
Üçgenin Alanı=10cm²‘dir.
7)Bir eşkenar, çeşitkenar, ikizkenar üçgenin çevrelerini nasıl bulurdunuz?(Formülleri)
Eşkenar Üçgen=3a
Çeşitkenar Üçgen=a+b+c
İkizkenar Üçgen=2a+b
8)Bir üçgenin özelliklerinden olan kenarları arasındaki bağlantıları genelleyin.
b+c>a , a+c>b , a+b>c Þİki kenarın uzunlukları toplamı üçüncü kenar uzunluğundan büyüktür.
b-c
Tarih: 2016-03-02 01:56:59 Kategori: Geometri
Kitaptan sorunu tarat hemen cevaplansın.
Yorum Yapx

 4 yıl önce
4 yıl önce

 8 yıl önce
8 yıl önce
 8 yıl önce
8 yıl önce
 8 yıl önce
8 yıl önce
 8 yıl önce
8 yıl önce
 8 yıl önce
8 yıl önce
 8 yıl önce
8 yıl önce
